2023-09-11-ListADT

Abstract data type(ADT) of LinkedList and ArrayList, code implementations, and comparison.

Singly Linked List

Basic data structure:

List.h

#pragma once
template <typename T>
class List {
private:
 class ListNode{
  T data;
  *ListNode next;
  ListNode(T & data): data(data), next(nullptr){};
 };
 *ListNode head_;
}

The structure of a ListNode is like: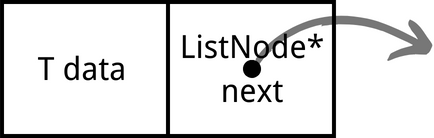

The structure of a LinkedList is like:

Basic operations:

1. insert at front;

List.hpp

template <typename T>
void List<T>::insertAtFront(const T& data) {
 ListNode* tmp = new ListNode(data);
 tmp->next = head_;
 head_ = tmp;
}

• Function inserts a new ListNode with the given data at the front of the list.
• Due to the data structure of a linked list, it is easy to insert at front of a LinkedList. it only takes O(1).
• We simply need to first create a new ListNode, then make the pointer in the new node point to the current head_. At last, make the head_ pointer point to the new node.

2. _index

List.hpp

template <typename T>
List<T>::ListNodeListNode *& List<T>::_index(int index) {
 return helper(index, head);
}
template <typename T>
List<T>::ListNodeListNode *& List<T>::helper(int index, ListNode *& root) {
 if (root == nullptr || index == 0) {
  return root;
 }
 return helper(index-1, root->next);
}

or

List.hpp

template <typename T>
List<T>::ListNodeListNode *& List<T>::_index(int index) {
 if (index == 0) {return head_;}
 ListNode* curr = head_;
 for (int i = 0; i < index - 1; ++i) {
  curr = curr->next;
 }
 return curr;
}

• The Function returns the node at the given index by a reference to the pointer.
• Note that the return type of _index is ListNode *&, a reference to a pointer to a ListNode . In this way, we can change the node the pointer is pointing to in the list in other functions.
• Both of the recursive or the iterative method need O(n) running time. The iterative method is favorable for lists with bigger size due to the call stack structure of the recursive method.

3. insert

List.hpp

template <typename T>
void List<T>::insert(int index, T data) {
 ListNode*& curr = _index(index);
 ListNode* tmp = new ListNode(data);
 tmp->next = curr;
 curr = tmp;
}

• The function inserts a node at given index with given data.
• First get the reference to the pointer pointing to the node at the given index using _index(index). The rest steps are like insertAtFront(), because it is the reference to a pointer returned from _index(index), changing the reference changes the pointer in the list.

4. random access

List.hpp

template <typename T>
T & List<T>::operator[](unsigned index) {
 ListNode*& curr = _index(index);
 return curr->data;
}

• The function returns the data of the node at the given index in the list.
• Returning the reference to the data considers the needs for a random access. User may hope to change the data at a specific index of a list.

5. find

List.hpp

template <typename T>
ListNode*& List<T>::find(T data) {
 return helper(head_, data);
}
template <typename T>
ListNode*& List<T>::helper(ListNode *& node, T data) {
 if (node->data == data || node == nullptr) {return node;}
 return helper(node->next, data);
}

• The function returns the reference to the pointer pointing to the node with given data.
• The runtime is O(n).

6. remove

List.hpp

template <typename T>
ListNode*& List<T>::remove(ListNode *& node) {
 Listnode * tmp = node;
 node = node->next;
 T data = temp->data;
 delete tmp;
 return data;
}

• Given the reference to the pointer, removing a ListNode takes O(1) running time. Other removals like remove(T data) or remove(unsigned index) can first use find(data) and _index(index) and then remove the ListNode (the running time increases to O(n)).

Pros and Cons of Linked List

Pros: it is easy to change the content of the list if we have the address to the nodes.

Cons: it is hard to get the address to the nodes, since the linked list is not a contiguous structure, and the only address directly stored is the head_.

Array List

Basic data structure:

ArrayList.h

template <typename T>
class ArrayList {
public:
private:
 T* data_;
 T* size;
 T* capacity;
}

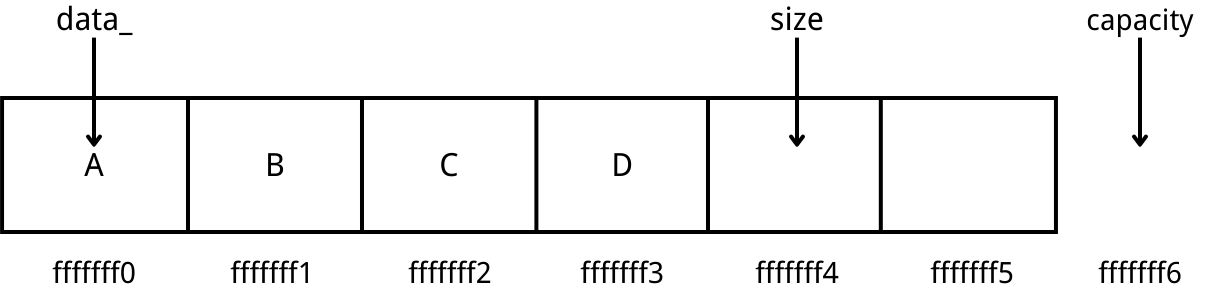
• Implementing the data_, size, and capacity as addresses (pointer) is more direct while inserting/removing items, and it does no harm. Number of items in an array can be calculated by (size - data_)/sizeof(T).

Basic operations:

1. random access

ArrayList.hpp

template <typename T>
T & ArrayList::operator[](unsigned int index){
 T * data = data_ + index*sizeof(T);
 return *data;
}

• takes O(1) running time.

2. insert at front

ArrayList.hpp

template <typename T>
void ArrayList::insertAtFront(T data){
 int back_index = (size - data_) / sizeof(T);
 for (; back_index > 0; --back_index) {
  (*this)[back_index] = (*this)[back_index - 1];
 }
 *data_ = data;
 size++;
}

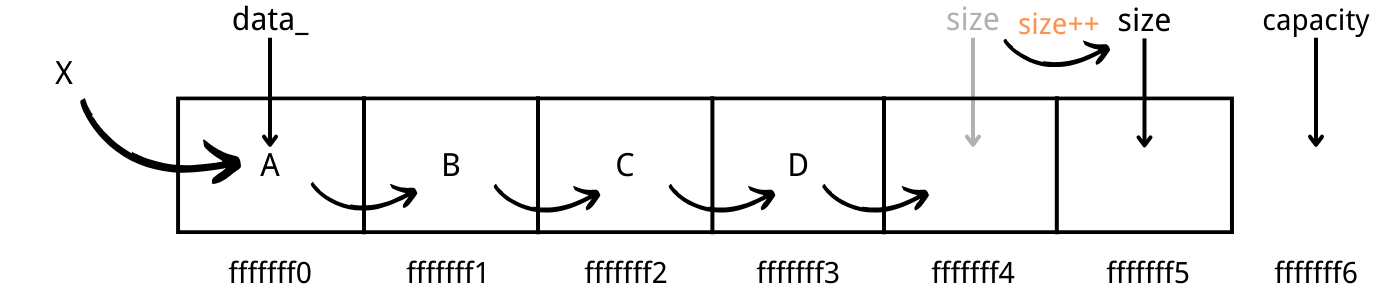
• ArrayList is not good at inserting at the front. It needs to shift every item backward, which takes O(n) running time.
• Even thought size is a pointer, size++ works by adding the address with the size of T, automatically pointing to the next available space for type T.

3. insert a given data at a given index

ArrayList.hpp

template <typename T>
void ArrayList::insert(int index, T data){
 int back_index = (size - data_) / sizeof(T);
 for (; back_index > index; --back_index) {
  (*this)[back_index] = (*this)[back_index - 1];
 }
 data_[index] = data;
 size++;
}

• Because of the structure of an ArrayList, it is complex to insert at indexes that already have data stored, which takes O(n) running time.

4. push back (insert at frist available space)

ArrayList.hpp

template <typename T>
void ArrayList::pushback(T data){
 *size = data;
 size++;
}

• However, if the data is to be stored in an available space in the back,** it takes only O(1) running time. ArrayList is good at inserting at back.**
• Additionally, popback() also takes only O(1) running time.

5. remove

ArrayList.hpp

template <typename T>
T ArrayList::remove(int index){
 size--;
 int back_index = (size - data_) / sizeof(T);
 T data = (*this)[index];
 for (; index < back_index; ++index) {
  (*this)[index] = (*this)[index + 1];
 }
 return data;
}

• Since after removing the item at the index, we need to shift all the following items forward for ArrayList (ArrayList is contiguous), it takes us O(n) to remove.
• If there are too many items in an ArrayList and we need to remove multiple times, instead of shifting the items and adjusting the size each time, we can first mark all the deleted items as “tombstone” using pointer and complete the shifting and calculating size all by once: number of items = (size - data_)/sizeof(T) - # of tombstones.

6. resizing strategy

Since an array is in memory adjacent, which means that it requires continuous memory allocation, once the capacity of an array is allocated, we cannot change it. When an array is growing out of the capacity, we will want to reallocate another array with larger capacity. Here comes the topic of this section: how much larger do we want our new array to be?

In the following paragraphs, the +2 resizing strategy (growing the capacity by 2 per reallocation) and the ⨉2 resizing strategy (multiplying the capacity by 2 per reallocation) and the comparison between their runtime are discussed.

• +2 elements strategy

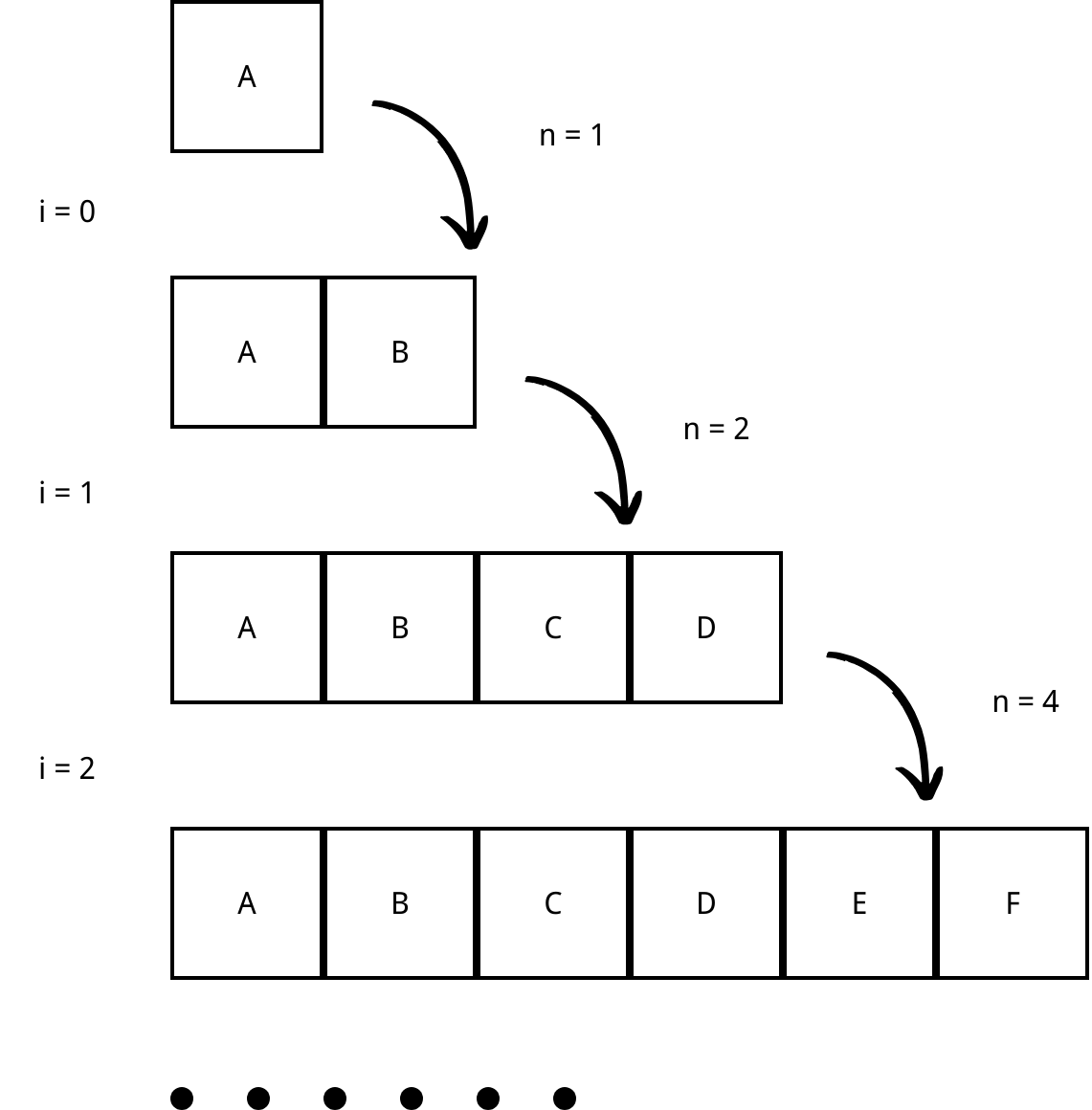
i: reallocation index

n: number of copies at a reallocation

We can tell that at a reallocation i, the total number of copies we have to make is 2i.

In order to encompass n items in an array, starting from an array with capacity 1, we have to increase the capacity by 2 for \( \frac{n}{2} \) times of reallocations. We can then calculate the number of copies we have to make increasing the capacity from 1 to n is $$\sum_{i=0}^k 2i = k(k+1) = \frac{n}{2}(\frac{n}{2}+1)$$

In summary, for the +2 elements resizing strategy, the total number of copies for making n insertins is \( \frac{n^2 + 2n}{4} \), so the expected copies for one insert is \( \frac{n+2}{4} \).

• ⨉2 elements strategy

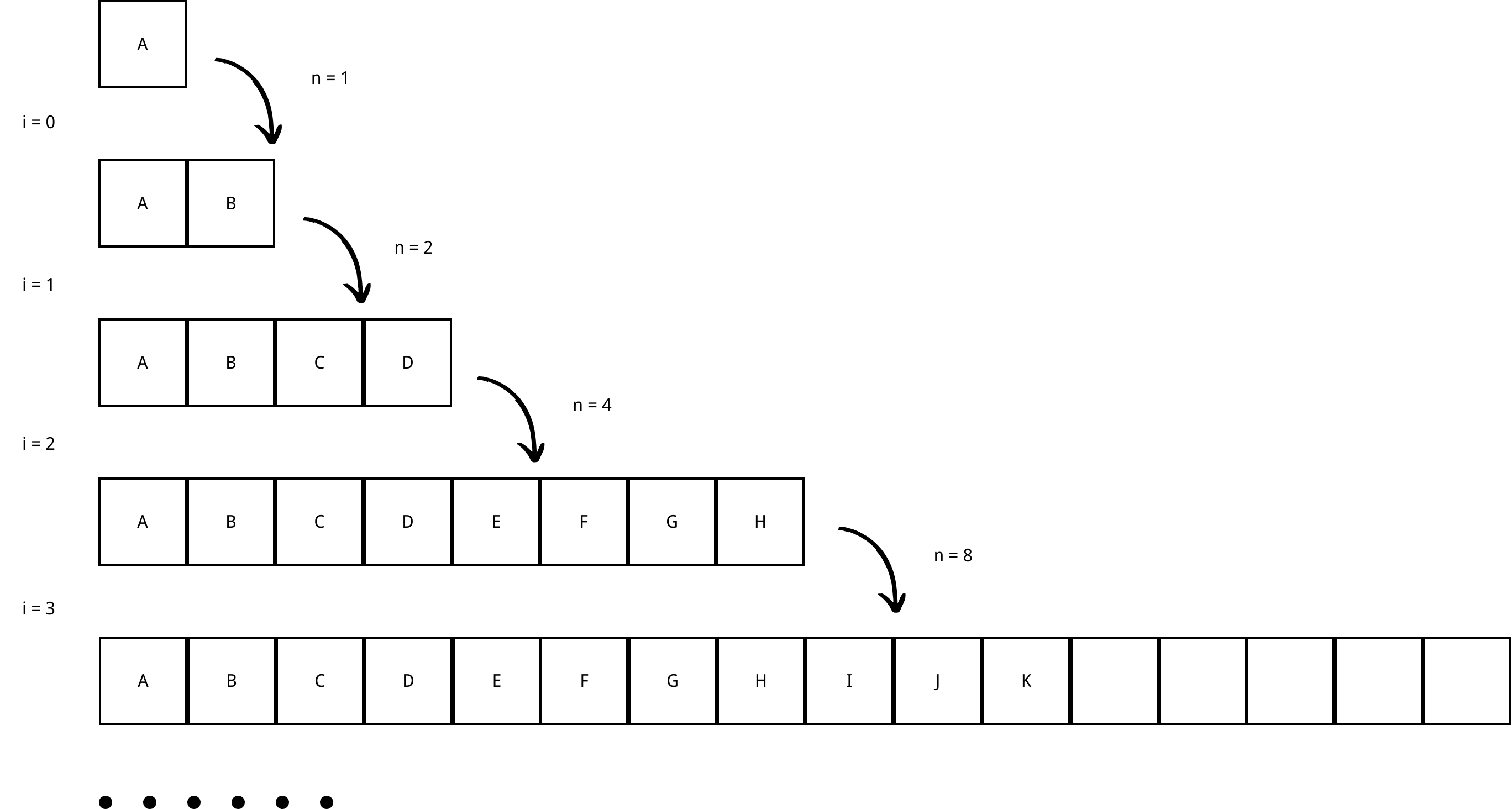
At a reallocation i, the total number of copies we have to make is \( 2^i \).

In order to encompass n items, we need to make sure that \( 2^k > n \), so the number of reallocation to encompass n items is \( k=ceil(\log _{2} n) \).

Total number of copies: $$\sum_{i=0}^k 2^i = 2^{k+1}-1 = 2^{\log _{2}{n}+1}-1 = 2n-1$$.
For *2 elements strategy the expected cost for one insert is \( 2-\frac{1}{n} \).


As shown above, the *2 emelments strategy is more effcient.

Array implementation

Basic implementations comparison:

	Sinlgly Linked list	Array List
Look up arbitrary location (random accessing)	O(n)	O(1)
Inset after given element	O(1) Don’t need to find where to insert	O(n)
Remove a given element	O(1)	O(n)
Insert at arbitrary location	O(n) Have to go through the linked list to find where to insert	O(n) worst case
Remove at arbitrary location	O(n)	O(n)
Search for an input value	O(n)	O(n)

Additional implementations:

Can we make our list better at some things? What is the cost?

• Currently getting the size of a linked list has a Big O of O(n)
  • We can add a private member unsigned size in List class, decreasing the running time of getting the size from O(n) to O(1)
  • The cost is that it increases memory and needs update: memory is increased by 4 bytes, update needs O(1).
• Currently the Linked List is unsorted
  • Sorting a linked list is applicable when we want a list that returns the smallest item becomes O(1).
  • The cost is that inserting into a sorted list becomes O(n), and some data structures aren’t applicable for sorting.
• Currently the list is singly linked
  • Making the list doubly linked simplifies removing at back to O(1).
  • Doubly linked list needs an additional pointer at each node, increasing the memory cost.