2023-09-25-StackAndQueue
Abstract data type(ADT) of Stack and Queue.
1. Stack data structure
With the advantage of the first available space at the back, the structure of array is best suited for the implementation of a stack.
A stack stores an ordered collection of objects, while the stack data structure only allows inserting or removing an item at the back: push() function puts an item on the top of the stack, and pop() function removes the item at the top of the stack.
Stack Abstract Data Structure
Order
Since the stack only push or pop the item on the top, the item put in later will be pushed out earlier, which means the stack has an order of Last In First Out (LIFO). This order leads to the concept of call stack, which plays an important role in recursion.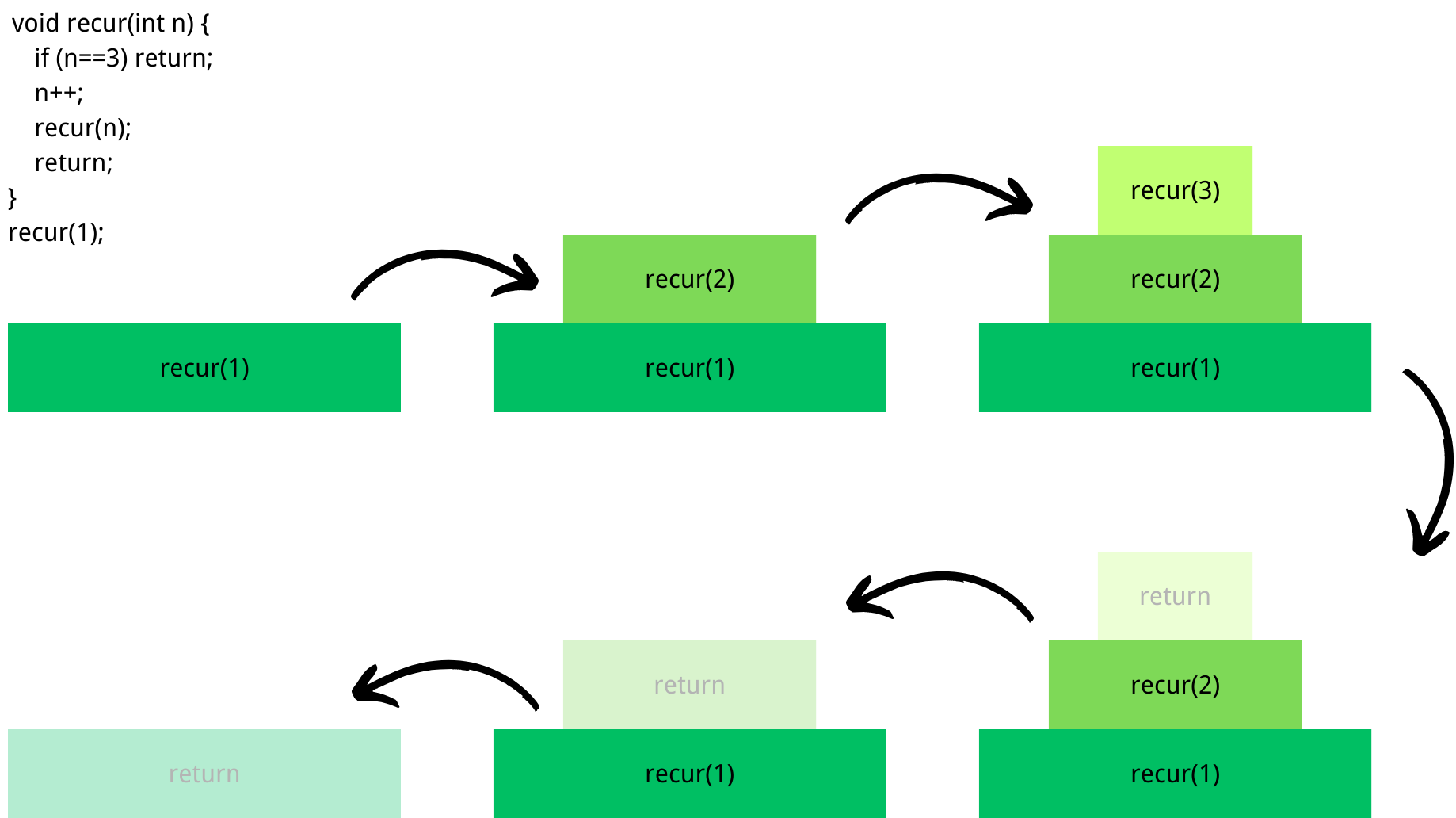
Implementation
C++ has its built-in stack structure, implemented using a vector or a double-ended queue.
Runtime
1 | template <typename T> |
With the pointer size pointing at the first available space at the back, push() takes only O(1) runtime.
1 | template <typename T> |
To remove the item on top, we must first make the size point to the last item. Then, we copy the data to pop out and remove the item from the list. This function also takes O(1) runtime.
2. Queue Data Structure
A queue stores an ordered collection of objects, but we are only allowed to perform two operations: enqueue () puts an item at the back of the queue, and dequeue() removes and returns the front item of the queue.
Queue Abstract Data Structure
Order
Since only inserting at the end and removing at the front are allowed, the item put in the list earlier is also removed earlier, which is a First In First Out (FIFO) order.
Implementation
Considering that we are going to remove items from the front, a Linked List structure seems to be a good choice for implementation. As for inserting at the front, we can add a tail_ pointer that points to the last item in the list, making enqueue() take O(1) runtime.
However, like in the stack structure, the vector or double-ended queue is also used to implement the queue data structure for following reasons:
- To make an array, we need only one pointer in regardless of the number of items in the list, while we need one pointer for an item to make a linked list. The pointers take more memory and make the operations prone to memory leak.
- The array uses continuous memory. The whole array can be accessed locally in the RAM (read faster than separated blocked linked list)
In order to track the queue behavior within an array, we have to change the size and end from pointer to unsigned int, and add another member: front_.
1 |
|
We want to implement a circular queue:
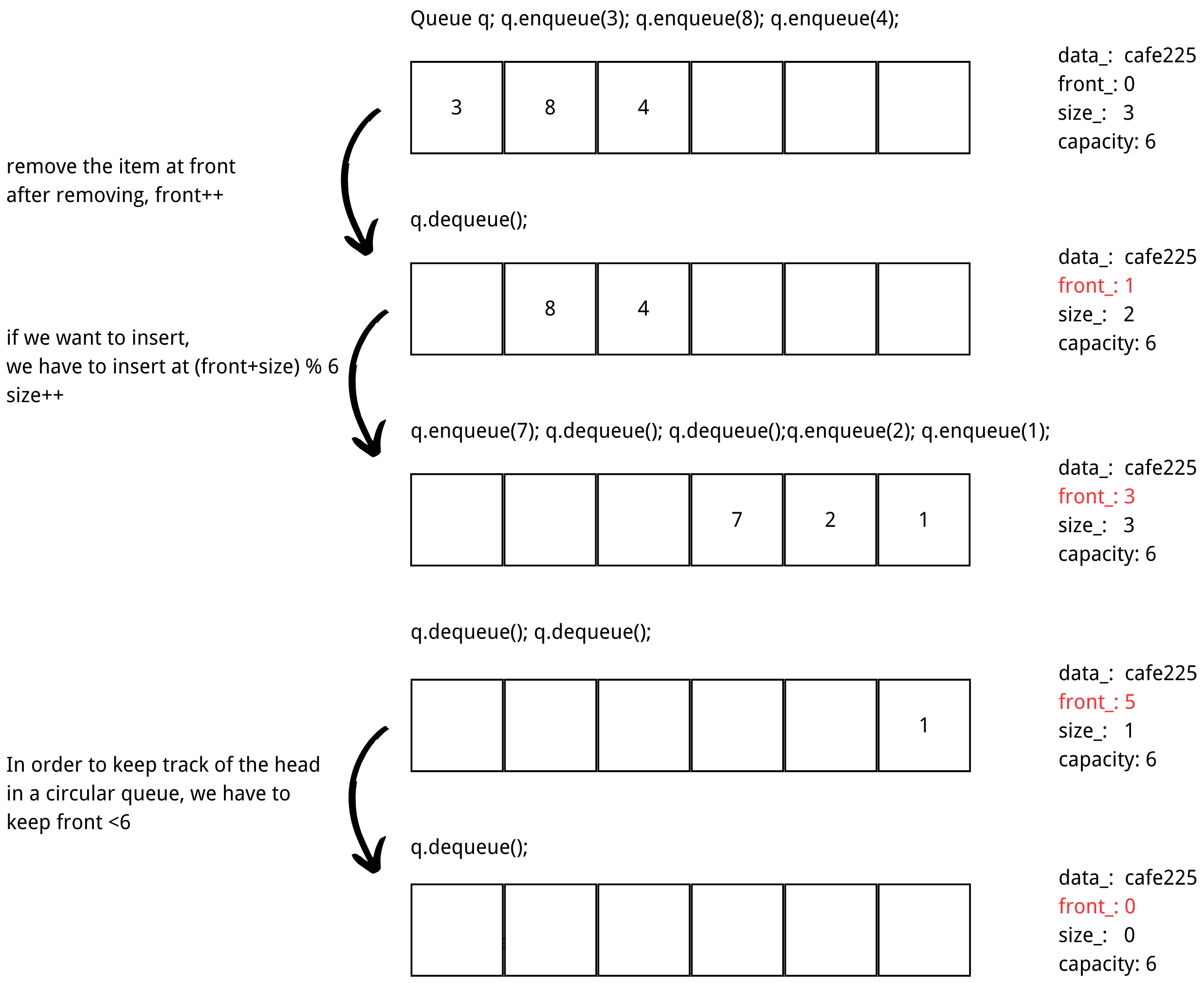
1 | template <typename T> |
In order to keep track of the first item in an circular queue, we have to make sure that \(front\_ < 6\) by making front = (front+1)%6 when increasing front.
As for resizing, when we copy the items in the original queue, we have to start from the item at front_ index to item at ((front_+size_)%capacity_ - 1) index to make sure the items stays in the same order.
Runtime
Both of the functions require O(1) runtime, while if we are inserting an item when the queue is full, we then have to resize the array, it takes O(n) runtime in the worst case.
2023-09-25-StackAndQueue
http://gong208.github.io/2023/09/25/2023-09-25-StackAndQueue/