2023-10-17-BinaryTree

Basic concepts about a binary tree.

Binary Tree

In this passage we are going to talk about another data structure: binary tree.

1. Binary Tree definition

BinaryTree.h

#pragma once 
template class 
BinaryTree { 
public: 
    /* ... */
private: 
    class TreeNode { 
        T & data; 
        TreeNode * left; 
        TreeNode * right; 
        TreeNode(T & data) : data(data), left(NULL), right(NULL) { } 
    }; 
    TreeNode *root_;
    /* ... */
};

The recursive definition of a binary tree:

• \( T = \lbrace \emptyset \rbrace \)
• \( T = \lbrace data, T_\text{left}, T_\text{right} \rbrace \)

\( T_\text{left} \) and \( T_\text{right} \) are the left and right subtrees, which are binary trees as well.

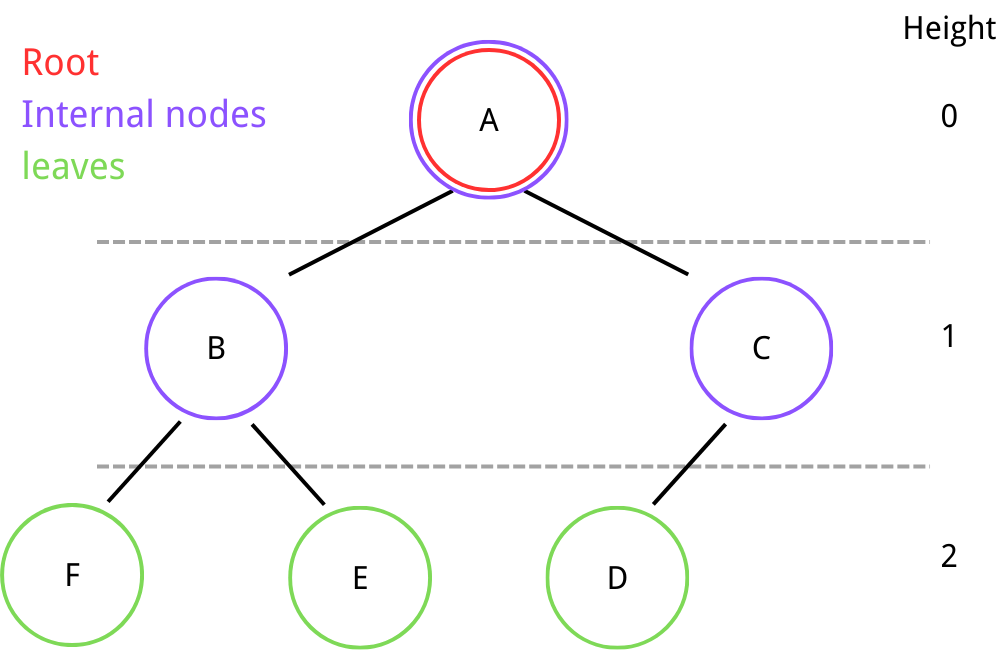
Height

The height of a node in a tree measures the shortest distance between the root and the node.

_height.cpp

#pragma once 
template class 
int BinaryTree::_height(TreeNode* subroot) { 
    if (subroot == NULL) return -1;
    return std::max(_height(subroot->left, _height(subroot->right))) + 1;
};

We define the height of a null node as -1.

Different types of binary trees and their recursive definition

1. A full binary tree

• \( T_{\text{full}} = \lbrace \emptyset \rbrace \)
• \( T_{\text{full}} = \lbrace \text{data}, \emptyset, \emptyset \rbrace \)
• \( T_{\text{full}} = \lbrace \text{data}, T_{\text{fullL}}, T_{\text{fullR}} \rbrace \text{ where both } T_{\text{fullL}} \text{ and } T_{\text{fullR}} \text{ are not } \emptyset \)

2. A perfect binary tree

Using h to represent the height of the node

• \( P_{\text{h}} = \lbrace data, P_{\text{h-1}}, P_{\text{h-1}} \rbrace \)
• \( P_{\text{h=-1}} = \lbrace \emptyset \rbrace \)

3. A complete tree

Using h to represent the height of the node

• \( C_{\text{h}} = \lbrace \text{data}, C_{\text{h-1}}, P_{\text{h-2}} \rbrace \)
• \( C_{\text{h}} = \lbrace \text{data}, P_{\text{h-1}}, C_{\text{h-1}} \rbrace \)
• \( C_{\text{h=-1}} = \lbrace \emptyset \rbrace \)

A complete tree is a tree with all levels filled except for the last level all nodes are pushed to the left.

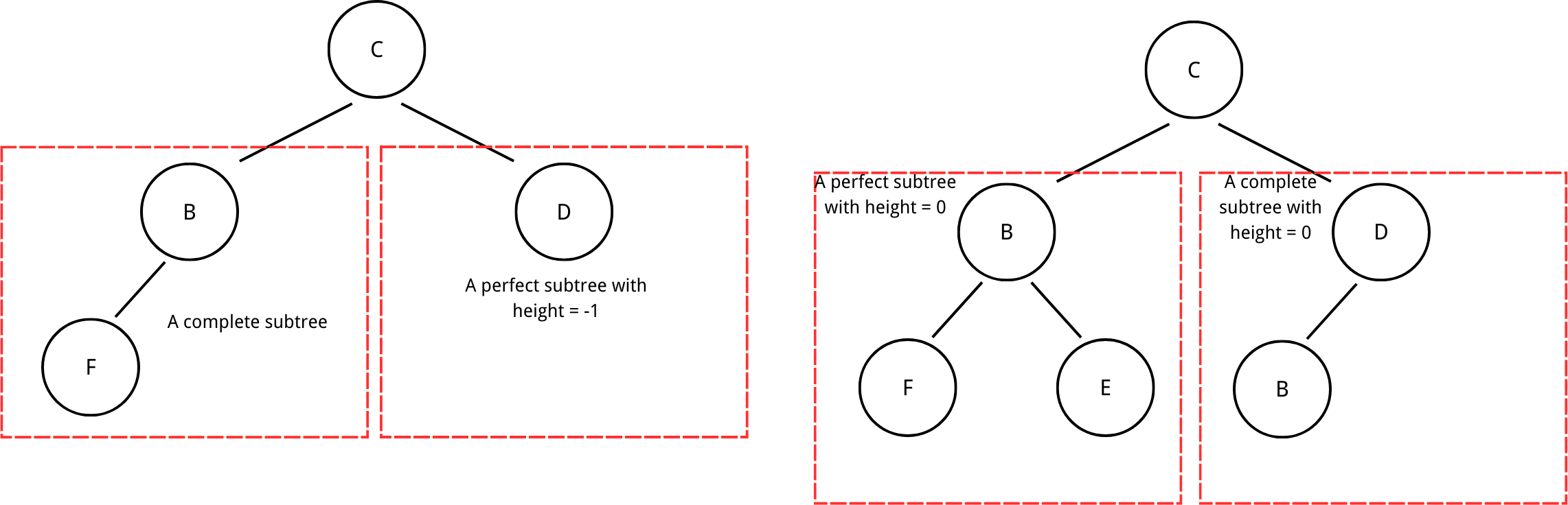
A perfect tree is a special case of a complete tree.

2. Binary Tree traversal

Traversal means that we visit every node in a tree once in a particular order. There are three types of traversals based on the order.

1. pre-order traversal

In a pre-order traversal, we process the data on the current node and then recursively visit the left and right node.

BinaryTree.hpp

template <typename T>
void BinaryTree<T>::preOrder(TreeNode * root) {
	//base case for empty list
	if (root == nullptr) return;

	_process(root);
	preOrder(root->left);
	preOrder(root->right);
}

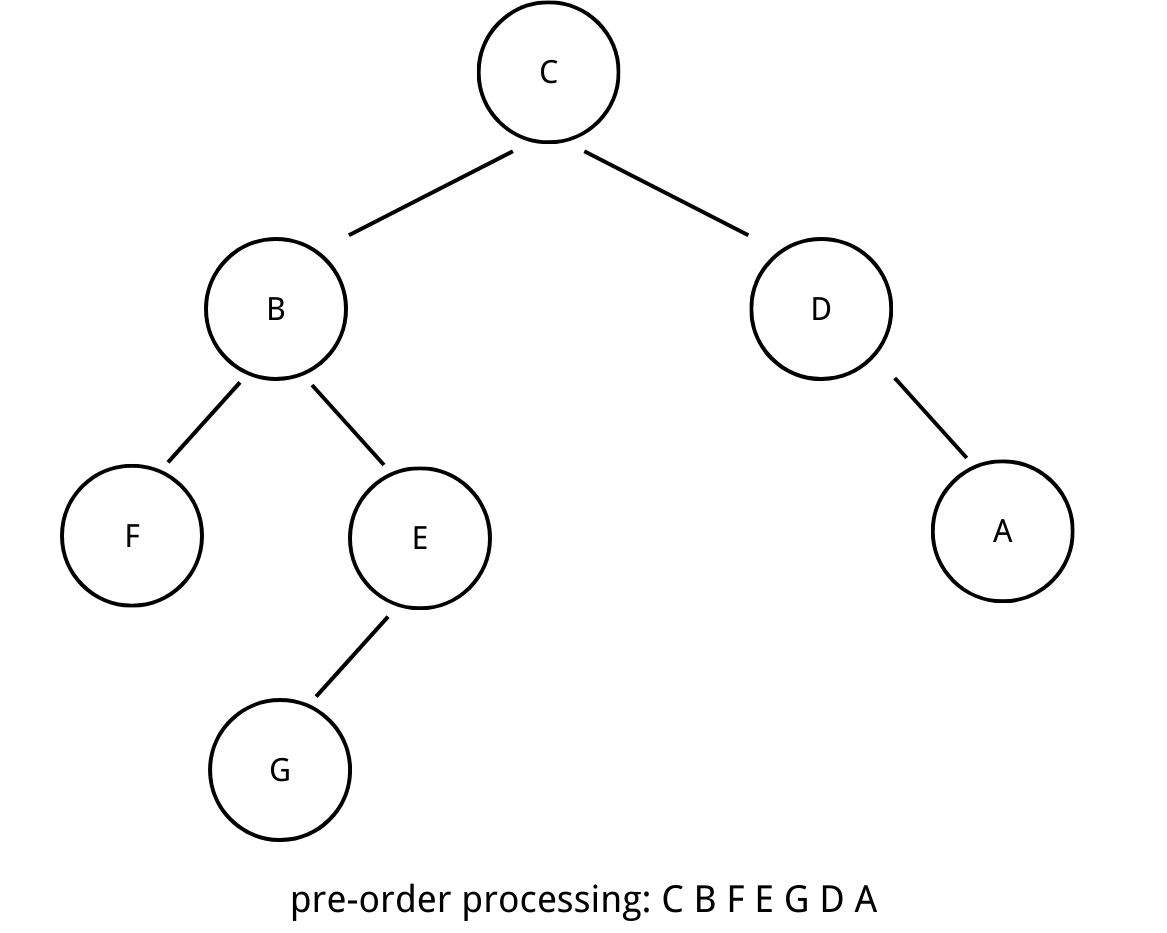
While constructing a tree by copying from another tree, it is ideal to use pre-order traversal: we construct the current node first and then we head to left and right child.

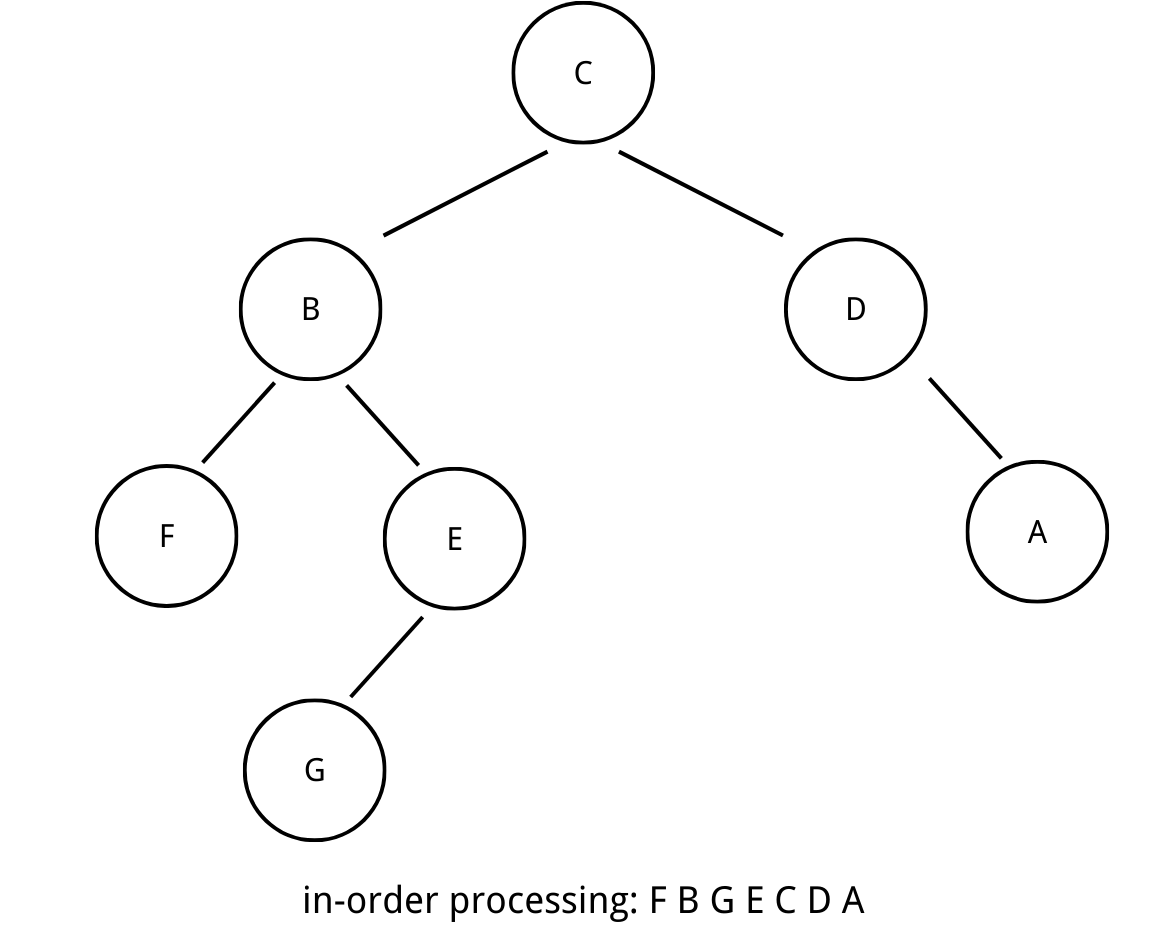
2. in-order traversal

The in-order traversal first visits the left child, upon return, process the data on current node, and then visit the right child.

BinaryTree.hpp

template <typename T>
void BinaryTree<T>::inOrder(TreeNode * root) {
	//base case for empty list
	if (root == nullptr) return;
	
	inOrder(root->left);
	_process(root);
	inOrder(root->right);
}

3. post-order traversal

In post-order traversal, we visit the left child. After returning from the recursion on left child, we visit the right child. We process the data on the current node at last.

BinaryTree.hpp

template <typename T>
void BinaryTree<T>::postOrder(TreeNode * root) {
	//base case for empty list
	if (root == nullptr) return;
	
	postOrder(root->left);
	postOrder(root->right);
	_process(root);
}

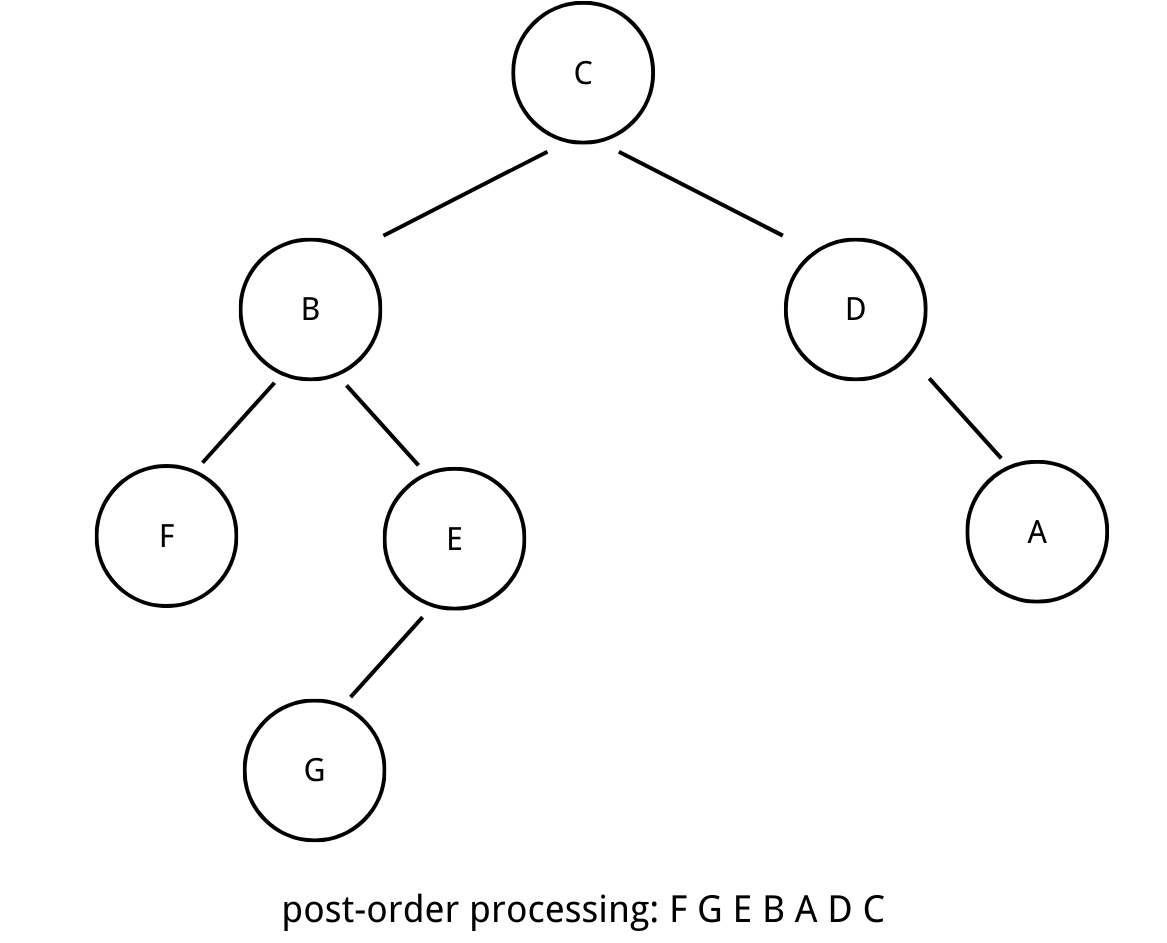
Since we process the current node at last, we can use a post-order traversal while deleting a tree: after we deleting the left subtree and right subtree, it is safe to delete current node.

3. Binary Tree search

We can search on a binary tree in two approaches: Depth-First Search and Breadth-First Search.

1. DFS

For DFS, we prioritize the depth in the sequence of search – we always explore as deep as we can.

BinaryTree.hpp

template <typename T>
void BinaryTree<T>::depth_first_search() {
	stack<TreeNode*> s;
	s.push(root); //initialize the stack with root
	while(!s.empty()) {
		TreeNode* tmp = s.top();
		s.pop();
		s.push(tmp->right);
		s.push(tmp->left);
	}	
}

This snippet of code only traverses the tree in the dfs order. To implement this order, we used a stack. Since the stack is Last In First Out order, we push the right child to the stack first and then the left child, thus the left child gets processed first.

2. BFS

For BFS, we explore the tree level by level (breadth).

BinaryTree.hpp

template <typename T>
void BinaryTree<T>::breadth_first_search() {
	queue<TreeNode*> q;
    q.push(root); //initialize the queue with root
    while(!q.empty()){
		TreeNode* tmp = q.front();
	    q.pop();
	    q.push(tmp->left);
        q.push(tmp->right);
    }	
}

The order of breadth-first search is also called level traversal. We use a queue instead of a stack since queue is First In First Out.

Currently, since a random node can be anywhere in a tree (the tree is not sorted), when we search for a node, we have to traverse through every node, which takes O(n) run time. If we want to avoid that, what shall we do?