2023-11-9-BinarySearchTree

Implementations and analysis of binary search tree.

Binary Search Tree

Basic definition

In the passage about binary trees, we want to improve the runtime for the search method. In order to find a node without traversing through the whole tree, we can make a sorted tree.

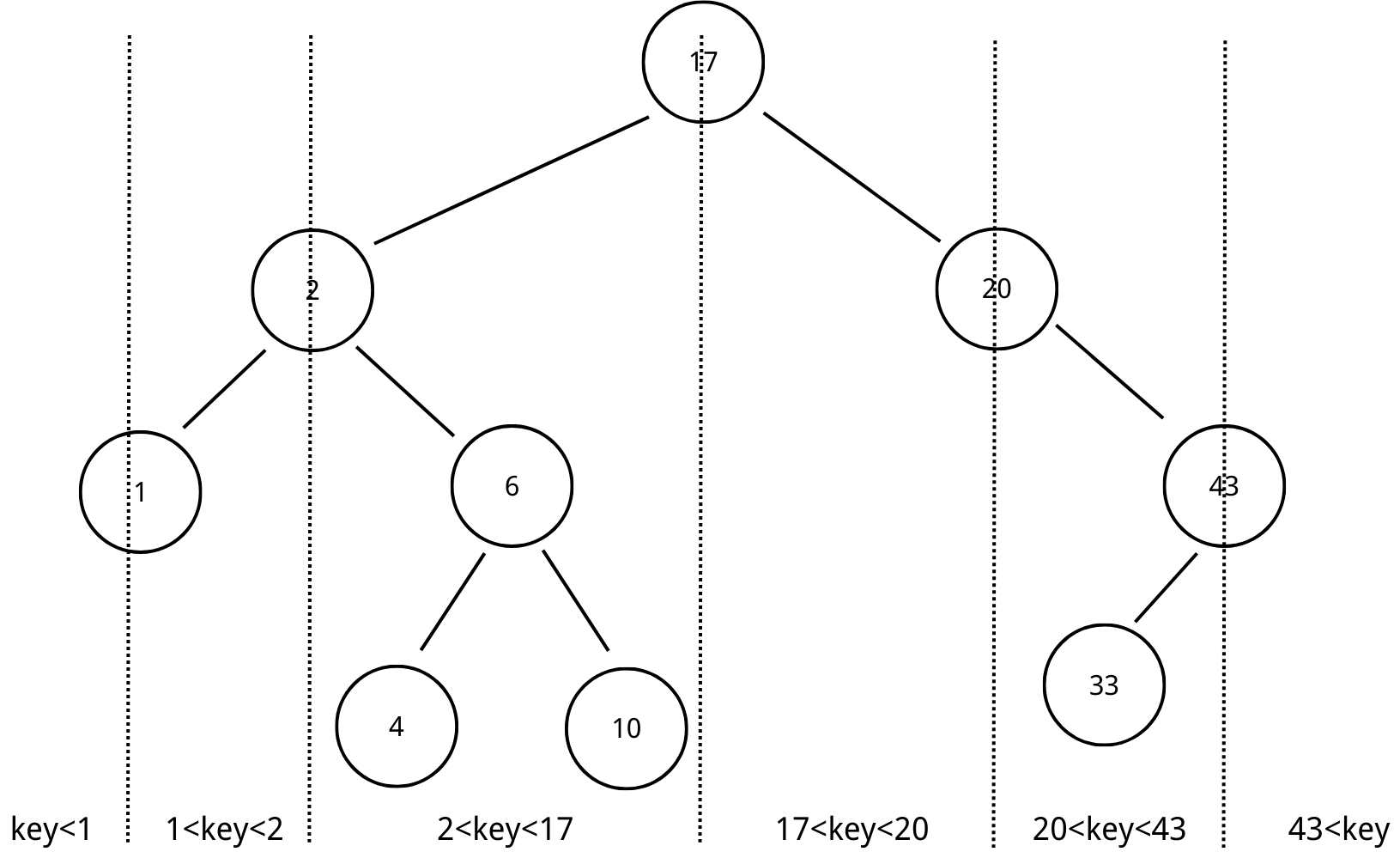
A binary search tree is defined as below:

• \( T = \lbrace \text{key}, T_{\text{left}}, T_{\text{right}} \rbrace \)
• All nodes to the left of a root have smaller keys than the root, and all nodes to the right of a root have greater keys.

BST.hpp

#pragma once 
template <typename K, typename V>
class BST { 
public: /* ... */ 
private: 
class TreeNode { 
     K & key; 
     V & value; 
     TreeNode* left;
     TreeNode* right; 
     TreeNode(K & k, V & v) : key(k), value(v), left(NULL), right(NULL) { };
}; 
     TreeNode *root_; 
/* ... */ 
};

BST implementations

BST find

Based on our definition of a binary search tree, we don’t have to traverse the whole tree while finding a key:

BST.hpp

template <typename K, typename V>
TreeNode*& BST<K,V>::_find (TreeNode *& root, const K & key) { 
     if (root == NULL || root->key == key) return root;
     if (root->key < key) return _find(root->right, key);
     return _find(root->left, key);
};

Since at every level, we make one comparison with the node and look for the subtree that potentially contains the query, the runtime of _find is O(h), in which h denotes the height of the tree.

BST insert

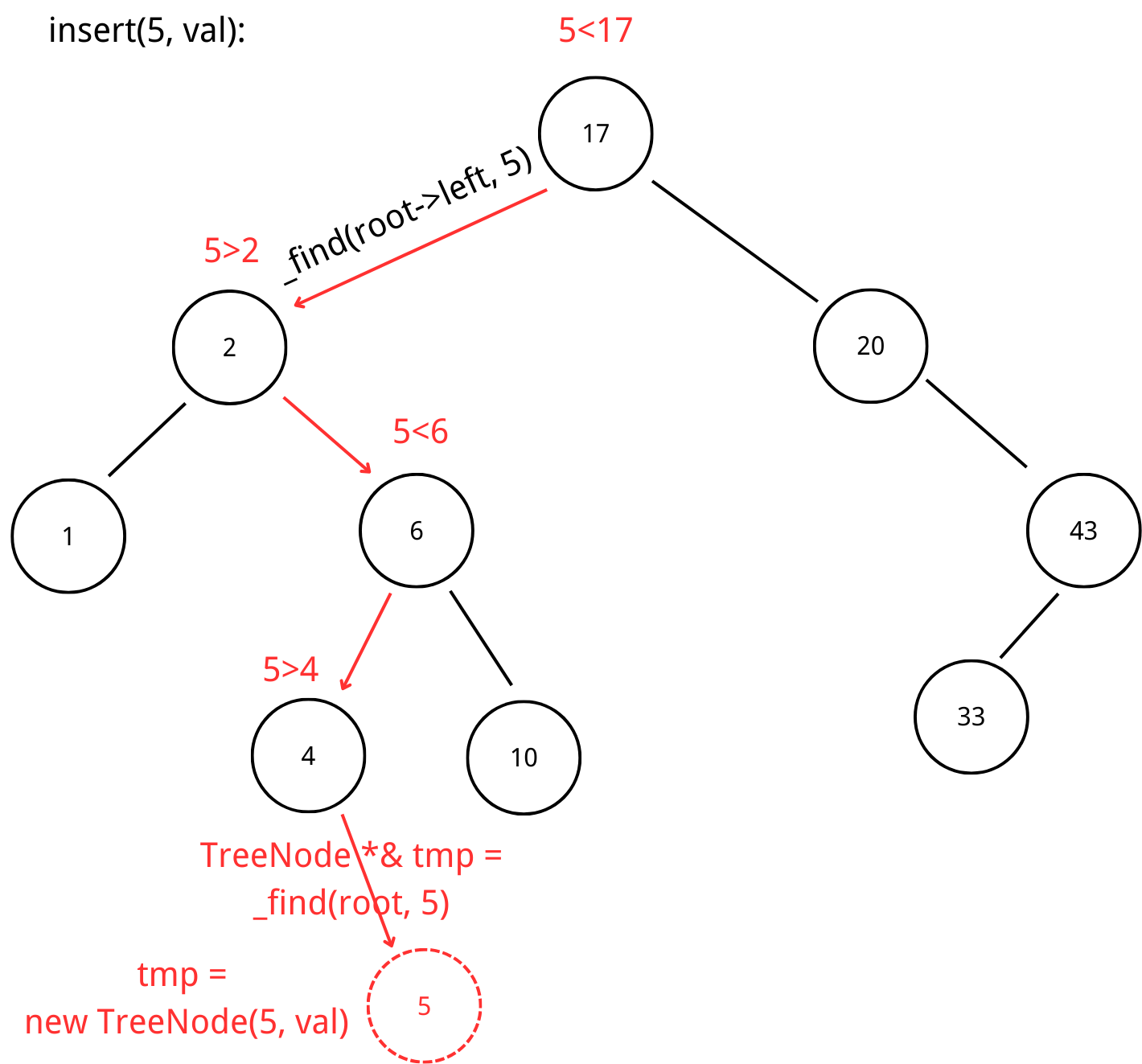
Since the _find function returns the **reference to the pointer, **we can first use the _find function to locate the position we want to insert and then directly create a new node.

BST.hpp

template <typename K, typename V>
void BST<K,V>::insert (const K & key, const V & val) { 
     TreeNode*& tmp = _find(root, key);
     tmp = new TreeNode(key, val);
};

Since insert() uses _find() and the additional step is only O(1), the running time for insert() is also O(h).

BST remove

Similarly, we can use _find(key) to find the node we are going to remove. However, we would want to preserve the feature of the BST after removing a node. There are three circumstances to consider.

No child remove

The simplest case is that the node we are going to remove has no child.

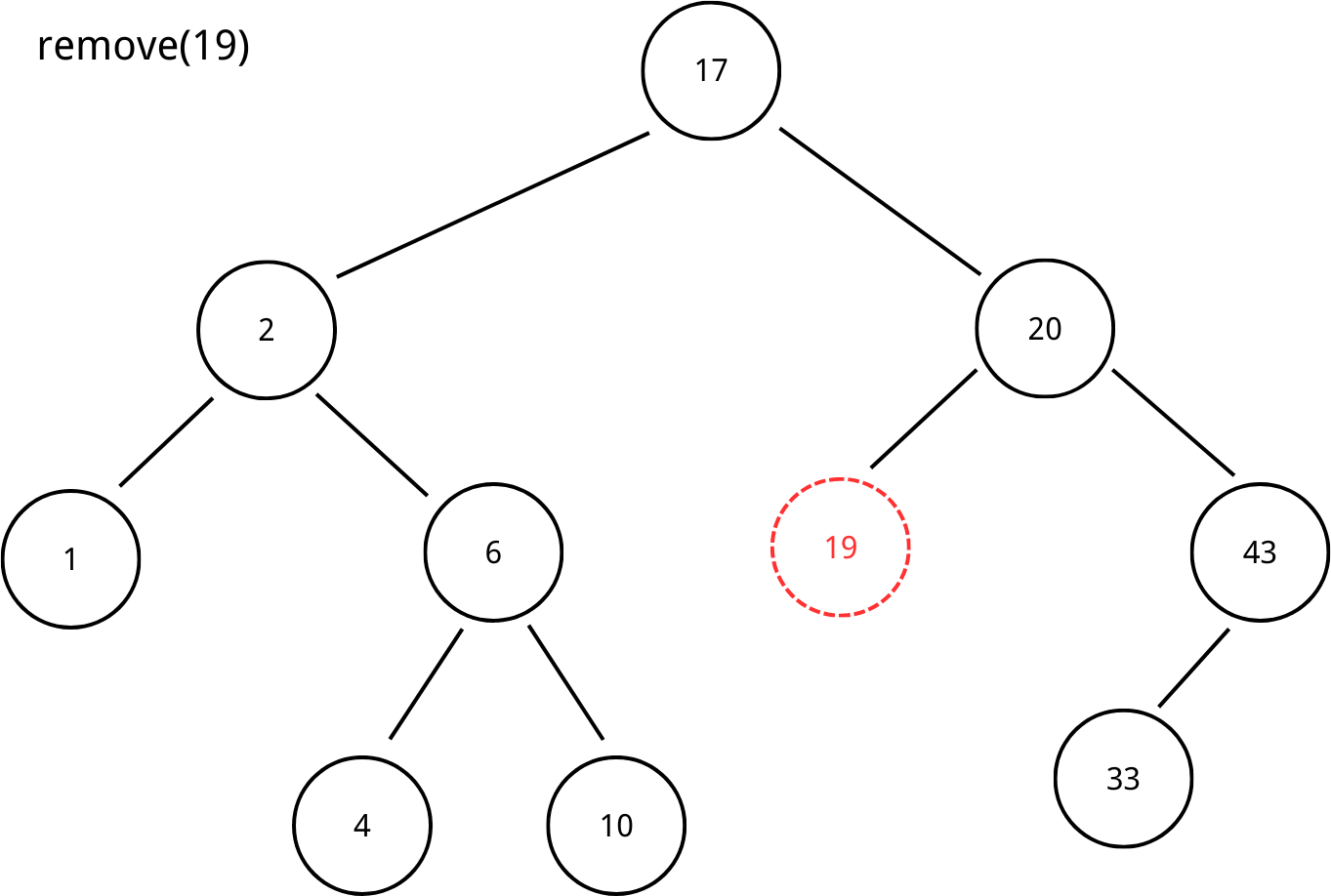
In this case, we can simply use _find() and deallocate the pointer to the node.

One-child remove

One-child remove is like the remove function of a linked list.

First, we allocate the place to remove with _find(), and preserve the node to be removed with a pointer. Using the reference to the pointer returned by _find(), we can replace the removed node with its only child.

Two-children remove

There are more things to consider when the node to be removed has two children: after the node is removed, which node are we going to fill in the blank so that we can still preserve the feature of the BST? (all the left children have keys smaller than the key in the subroot and all right children have keys larger than the key in the subroot)

BST.hpp

template <class K, class V>
void BST<K, V>::swap(Node*& first, Node*& second)
{
    // your code here
    K copy_key = second->key;
    V copy_value = second->value;
    second->key = first->key;
    second->value = first->value;
    first->key = copy_key;
    first->value = copy_value;
}

template <class K, class V>
BST<K, V>::Node* & BST<K, V>::findIOP(Node*& left) {
    // your code here
    if (left->right == NULL) return left;
    return findIOP(left->right);
}

template <class K, class V>
BST<K, V>::Node* & BST<K, V>::findIOS(Node*& right) {
    // your code here
    if (right->left == NULL) return right;
    return findIOS(right->left);
}

As shown in the graph, if we remove the node with key 17, the possible keys that fit in the blank location are values from 10 to 19. Additionally, we would want to replace the removed node with nodes existing in the tree instead of constructing a new node, so the two available nodes for replacing node(17) is node(10) and node(19). Generally, they are the in-order predecessor (the largest key smaller than the subroot) and in-order successor (the smallest key larger than the subroot).

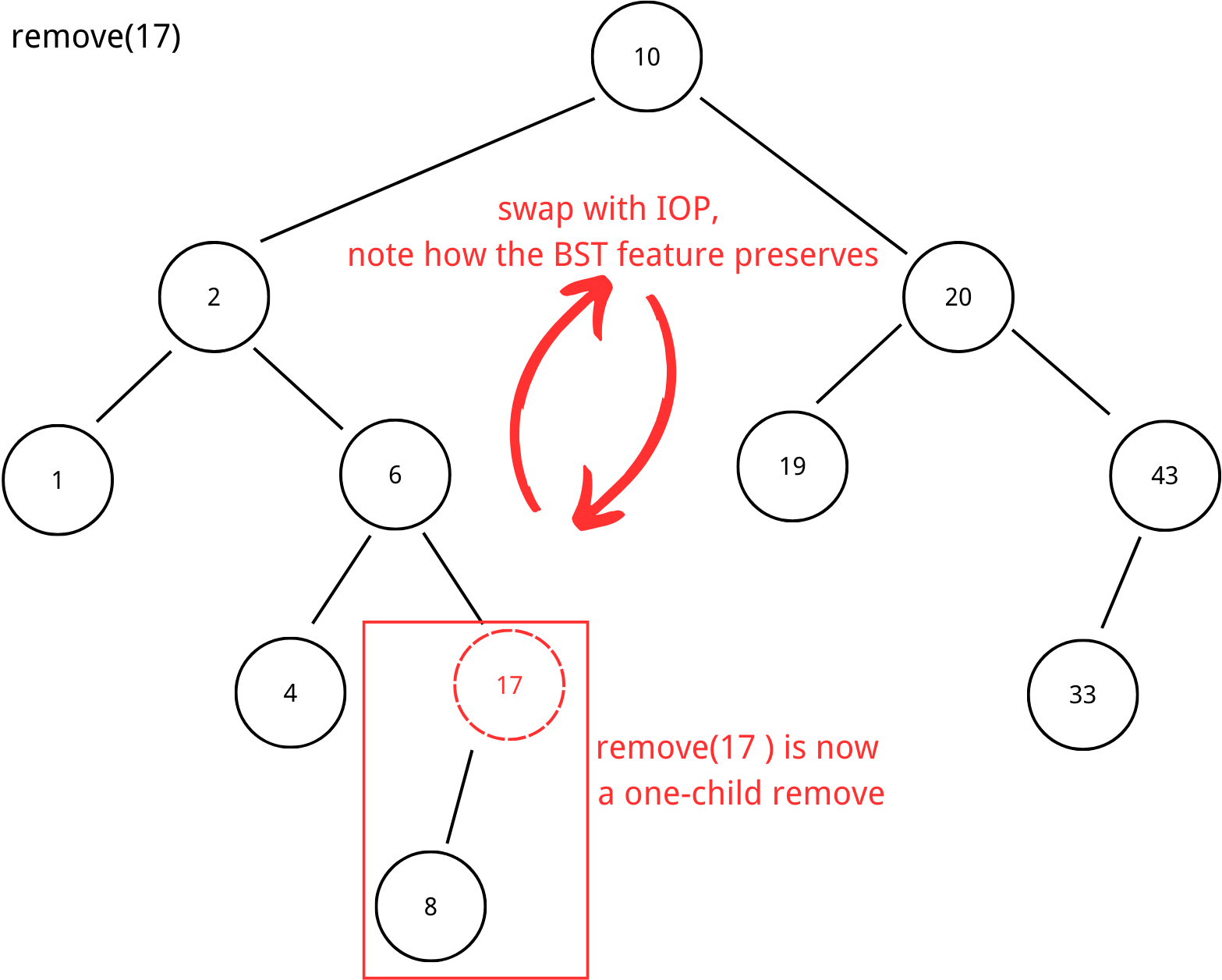
In summary, for two-children removal, after finding the mode to remove, we find either the IOP or the IOS with respect to the node. We then swap the subroot (removal node) with the IOP/IOS, which still preserves the feature of BST. At last, we call remove on the removal node again, but this time, it is either a zero-child remove or a one-child remove.

As for remove(), we can see that we first use _find(), which is O(h), and we also have to find IOP/IOS, which is another O(h). The swapping is only O(1). In summary, the running time for remove() is O(h).

BST.hpp

template <class K, class V>
void BST<K, V>::remove(Node*& subtree, const K& key)
{
    TreeNode *& to_remove = find(subtree, key);
    if (to_remove == NULL) return;
    //0 child remove
    if (to_remove->left == NULL && to_remove->right == NULL) {
        delete to_remove;
        to_remove = NULL;
        return;
    }
    //1 child remove
    if (to_remove->left == NULL && to_remove->right != NULL) {
        Node * tmp = to_remove;
        to_remove = to_remove->right;
        delete tmp;
        return;
    } else if (to_remove->left != NULL && to_remove->right == NULL) {
        Node * tmp = to_remove;
        to_remove = to_remove->left;
        delete tmp;
        return;
    }
    //2 children remove
    Node *& in_order_pred = findIOP(to_remove->left);
    swap(in_order_pred, to_remove);
    if (in_order_pred->left == NULL) {
        delete in_order_pred;
        in_order_pred = NULL;
    } else if (in_order_pred->left != NULL) {
        Node * tmp = in_order_pred;
        in_order_pred = in_order_pred->left;
        delete tmp;
    }
}

BST running time analysis

implementation	running time
find	O(h)
insert	O(h)
remove	O(h)
traverse	O(n)

Now, most of the implementations run in O(h) time, but what exactly is O(h)?

To answer this question, we have to relate h, the height of a BST, to n, the number of nodes in a BST.

We can see that for a BST with n = 5, the height varies by the sequence in which the nodes are inserted. More generally, for a given n, h has an upper bound of O(n), when the nodes are arranged like a singly linked list, and a lower bound of O(logn), when almost every level at height i is fully loaded with 2^i nodes.

Although both forms are valid BST, there is no doubt that the form that guarantees the running time of O(logn) is preferable.

Then how can we modify our tree to guarantee the ideal running time?