2025-05-03-Scan

What is scan?

In the previous post we introduced reduction, which is an operation that applies on a set of inputs to get a single value. Scan is a little more complicated which requries to output the prefix-sum array.

An inclusive scan

Given a sequence \( a_0, a_1, a_2, \ldots, a_{N-1} \), the inclusive scan returns the prefix-sum array \( b_0, b_1, b_2, \ldots, b_{N-1} \) such that \( b_i = b_{i-1} + a_i \).

Kogge-Stone Inclusive Scan

Data mapping

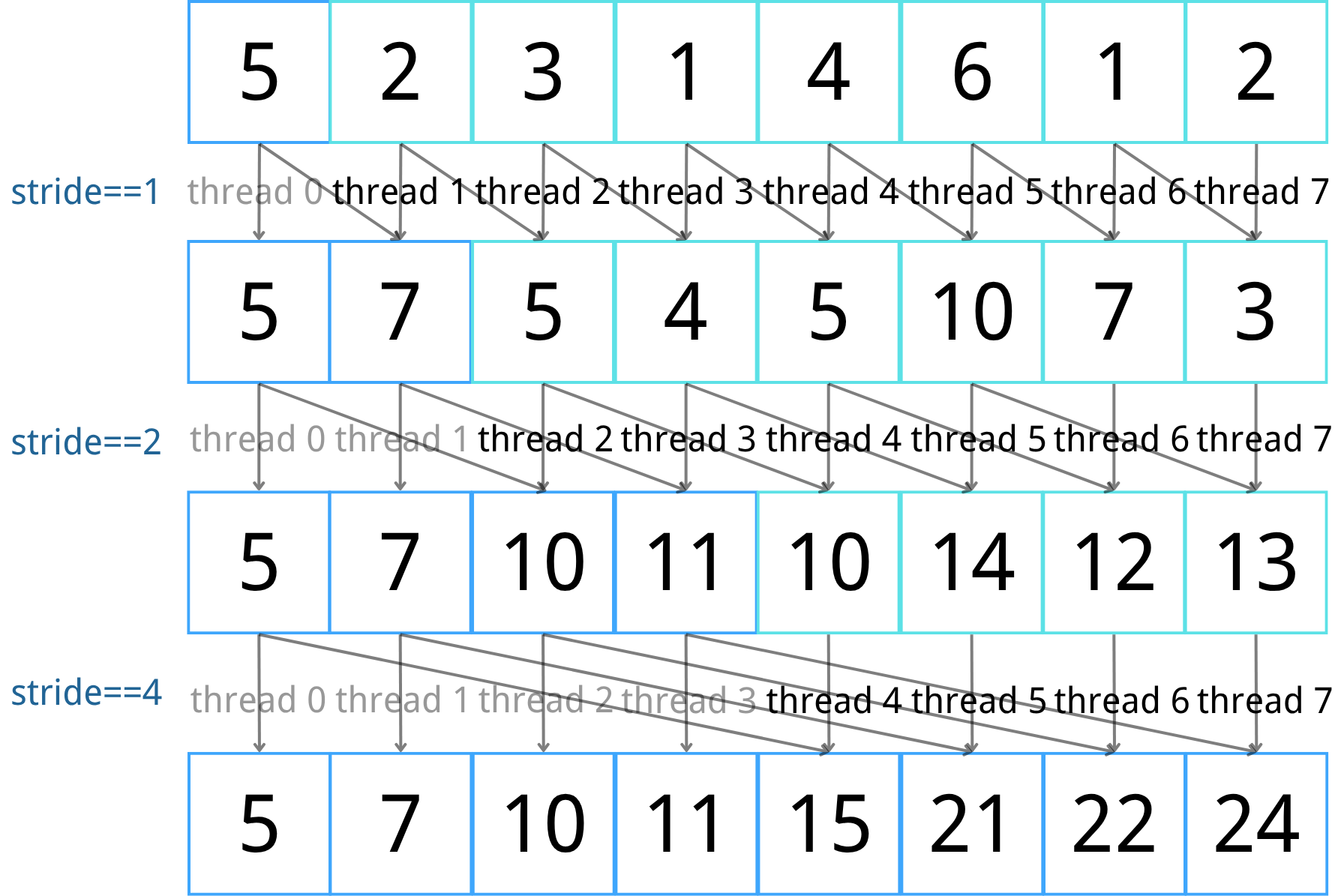
Each thread in a block is responsible for calculating a prefix-sum for a segment of the input array. So for a block with M threads it is able to scan M input elements.
Again, we start the \( stride \) from 1 and multiply it by 2 in each step. As such, in each step an active thread will compute sum of two sums over number of stride elements: array[threadIdx.x] += array[threadidx.x - stride], and in each step the first \( stride \) threads finisehd their computation for prefix sum.

__global__ void kogge_stone_scan(float *input, float *output, int len) {
    __shared__ float T0[BLOCK_SIZE];
    __shared__ float T1[BLOCK_SIZE];
    __shared__ bool reverse;
    if (threadIdx.x == 0) reverse = false;
    __syncthreads();

    int i = blockIdx.x * blockDim.x + threadIdx.x;
    if (i < len) {
        T0[threadIdx.x] = input[i];
    } else {
        T0[threadIdx.x] = 0.0f;
    }
    __syncthreads();
    for (unsigned int stride = 1; stride < blockDim.x; stride *= 2) {
        if (!reverse) {
            if (threadIdx.x >= stride)
                T1[threadIdx.x] = T0[threadIdx.x] + T0[threadIdx.x - stride];
            else
                T1[threadIdx.x] = T0[threadIdx.x];
        } else {
            if (threadIdx.x >= stride)
                T0[threadIdx.x] = T1[threadIdx.x] + T1[threadIdx.x - stride];
            else
                T0[threadIdx.x] = T1[threadIdx.x];
        }
        if (threadIdx.x == 0) reverse = !reverse;
        __syncthreads();
    }
    if (i < len) {
        output[i] = reverse ? T1[threadIdx.x] : T0[threadIdx.x];
    }
}

Analysis

A Kogge-Stone scan kernel executes \( log(N) \) steps, for each step \( (N-1), (N-2), (N-4), …, (N-N/2) \).
So there will be a total of \( N * log(N) - (N-1) \) operations.

Brent-Kung Inclusive Scan

Data mapping

Brent-Kung scan contains two steps: reduction step and the post scan step. Each threads is responsible for loading in two global elements and computing the prefix sum.

__global__ void Brent_Kung_scan(float *input, float *output, int len) {
  __shared__ float T[2*BLOCK_SIZE];

  int idx = 2 * blockIdx.x * blockDim.x + threadIdx.x;
  if (idx < len) {
    T[threadIdx.x] = input[idx];
  } else {
    T[threadIdx.x] = 0.0f;
  }
  
  if (idx + blockDim.x < len) {
    T[threadIdx.x + blockDim.x] = input[idx + blockDim.x];
  } else {
    T[threadIdx.x + blockDim.x] = 0;
  }

  __syncthreads();
  int stride = 1;
  while (stride < 2 * BLOCK_SIZE) {
    int index = (threadIdx.x + 1) * stride * 2 - 1;
    if (index < 2 * BLOCK_SIZE && (index - stride) >= 0) T[index] += T[index-stride];
    stride = stride * 2;
    __syncthreads();
  }

  __syncthreads();

  stride = BLOCK_SIZE / 2;
  while (stride > 0) {
    int index = (threadIdx.x + 1) * stride * 2 - 1;
    if ((index + stride) < 2 * BLOCK_SIZE) T[index + stride] += T[index];
    stride = stride / 2;
    __syncthreads();
  }

  if (idx < len) {
    output[idx] = T[threadIdx.x];
  }
  
  if (idx + blockDim.x < len) {
    output[idx + blockDim.x] = T[threadIdx.x + blockDim.x];
  }
}

Analysis

Brent-Kung scan executes \(2log(N)\) steps, with a total of \(2*(N - 1) - log(N)\) operations.

Comparison

The Brent-Kung scan only needs half of the number of threads than the Kogge-Stone scan, while the Kogge-Stone scan takes halve the number of steps compared to the Brent-Kung scan.

References

ECE408/CS483 University of Illinois at Urbana-Champaign
David Kirk/NVIDIA and Wen-mei Hwu, 2022, Programming Massively Parallel Processors: A Hands-on Approach
CUDA C++ Programming Guide